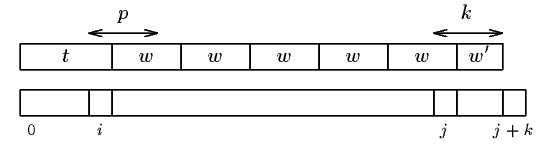
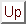During an attempt where the window is positioned on the text factor y[j .. j+m-1], when a prefix u of x has been matched and a mismatch occurs between characters a in x and b in y (see figure 26.1), the algorithm tries to compute the period of ub, if it does not succeed in finding the exact period it computes an approximation of it.

Figure 26.1: Typical attempt during the String Matching on an Ordered Alphabet algorithm.
- Let us define twew' the Maximal-Suffix decomposition (MS-decompostion for short) of the word x if:
-

v = wew' is the maximal suffix of x according to the alphabetical ordering; -

w is basic; -

e 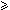 1;
1; -

w' is a proper prefix of w.
Then we have |t| < per/>(x).
If twew' is the MS-decomposition of a nonempty word x then the four properties hold:
-

if t is a suffix of w then per(x) = per(v); -

per(x) > |t|; -

if |t| 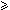 |w| then per(x) > |v| = |x|-|t|;
|w| then per(x) > |v| = |x|-|t|; -

if t is not a suffix of w and |t| < |w| then per(x) > min(|v,|twe|).
If u is a suffix of w then per(x)=per(v)=|w|.
Otherwise per(x) > max(|u,min(|v|, |twe|)) 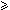 |x|/2.
|x|/2.
If twew' is the MS-decomposition of a nonempty word x, per(x) = |w| and e > 1 then If twe-1w' is the MS-decomposition of x' = uwe-1w'.
The algorithm computes the maximal suffix of the matched prefix of the pattern appended with the mismatched character of the text after each attempt. It avoids to compute it from scratch after a shift of length per(w)$ has been performed.
The String Matching on Ordered Alphabets needs no preprocessing phase.
The searching phase can be done in O(n) time complexity using a constant extra space. The algorithm performs no more than 6n+5 text character comparisons.